
Starting with a high-quality math program
In her research article, “Examining Key Concepts in Research on Teachers’ Use of Mathematics Curricula”, Janine Remillard described curriculum use as a dynamic and ongoing relationship between teachers and resources—a relationship shaped by both the teacher and characteristics of the resource.
I have found that while certain characteristics can make a math curriculum high-quality, it is only through its relationship with teachers that it creates truly meaningful math experiences for students.
In my own teaching experiences and now back in classrooms with teachers, I am convinced that no matter how well-constructed a lesson, it only gets better as teachers plan collaboratively and center their students.
Shaping lessons for the students in your classroom can be challenging because there is not one right way or time to adapt a lesson, and the reasons we adapt vary.
Sometimes we make relatively small tweaks to the wording of a prompt, a question the teacher should pose, or the timing of an activity.
Other times we make more substantial changes to the task or task structure in order to more clearly move toward the learning goal based on what we are seeing and hearing from students.
And then there are the times we realize in the midst of an activity we should have made an adaption in our planning.
I recently taught a 5th grade fractions lesson that provided a perfect example of the dynamic nature of the work.
Engaging in a math curriculum activity
This particular lesson falls at the end of the fraction addition and subtraction unit.
The Warm-Up of this lesson is a Number Talk, which made sense to the 5th grade teachers and I, given the unit focus.
We reviewed the mathematical concepts and problems in our planning session, anticipated that students might find common denominators, and agreed that the synthesis discussion around denominator choice aligned with the problems.

While we anticipated that students would successfully add, the number choices in the string led students to solve each one the same exact way, with the only difference being whether they stated their sum in simplest form or not.
Halfway through, we could see the majority of the students were getting bored and it was hard to infuse curiosity and excitement around denominator choice because students had already generalized a way of finding a common denominator—which at this point in the unit was great!
In the midst of the Number Talk, we paused and debated pivoting our focus to the problems in relation to one another rather than denominator choice. But we knew that doing that would add extra time to the lesson, when we needed the majority of the time for the activities that followed.
So we wrapped it up and moved on, knowing we had time to discuss our choice in an upcoming planning session.
Adapting in ways that center student ideas
After class, I couldn’t stop thinking about revisions I would make if we had the opportunity to plan it all over again. Because although the problems in the string supported mental calculation and aligned with the lesson activities, the students needed something different at this point in their learning.
After reflecting with colleagues, we decided the timing of that particular Number Talk for these students was too late in the unit and wondered if a different routine would have made it more engaging.
Using that Number Talk as a rough draft (shout out to Mandy Jansen), I played around with different number choices and routines we might use in a second take on that lesson.
If we wanted to stick with the same task structure, we could adjust the numbers to create a new Number Talk or True or False? routine that more explicitly encouraged relational reasoning and use of the properties.
For example, the following problem strings still attend to denominators when adding fractions but also open up the space for more interesting and engaging student discourse.
Number Talk

True or False?

If we wanted to use a different structure altogether, we could try the Which One Doesn’t Belong? routine to provide opportunities for students to notice other interesting aspects.
In this activity, students share reasons why one of four items—in this case, equations—doesn’t belong. There is no single right answer because each object could both belong and not belong, depending on the student’s criteria. (If you’ve never tried this routine, it’s a must!)
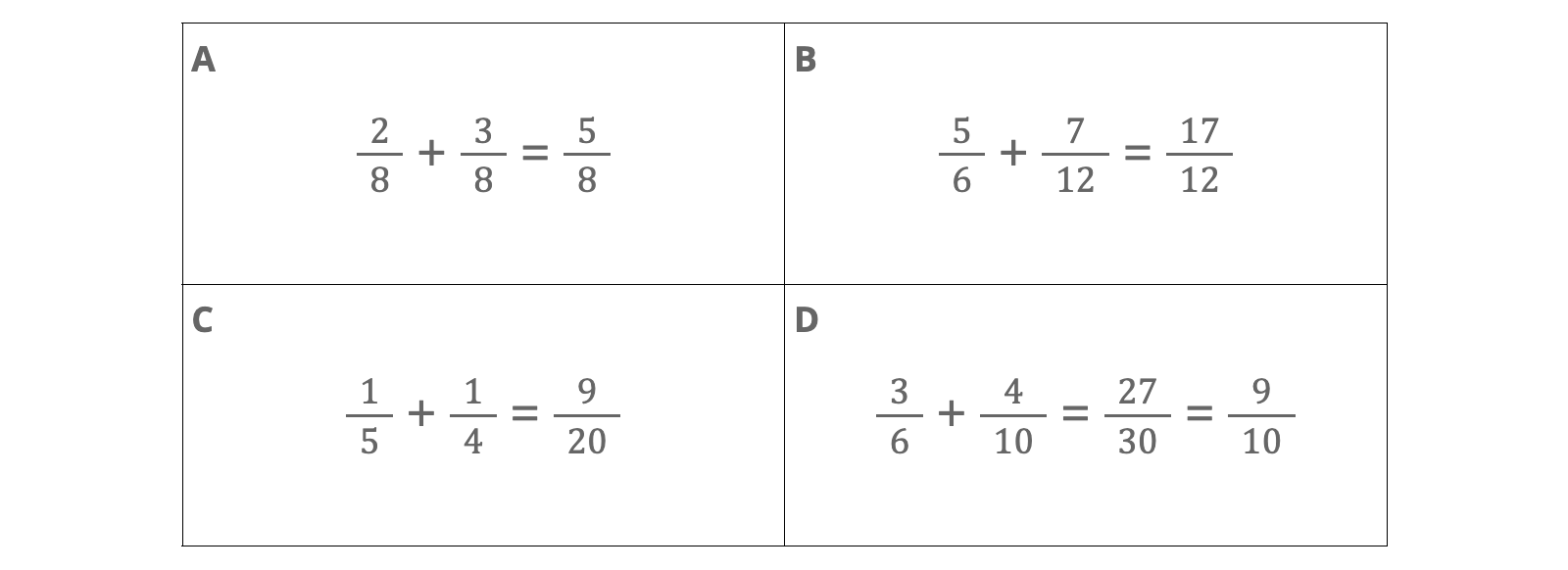
Because I couldn’t wait until this lesson next year to see what students would do with one of these ideas, I asked them to write about the Which One Doesn’t Belong? The variation among their ideas was exciting.
While I could still see attention to the denominators as in the original Warm-Up, students were now describing their ideas in much more unique ways. If this had been the original Warm-Up, it’s not hard to imagine how much more engaged students would have been—and how much more teachers would have learned about their thinking.





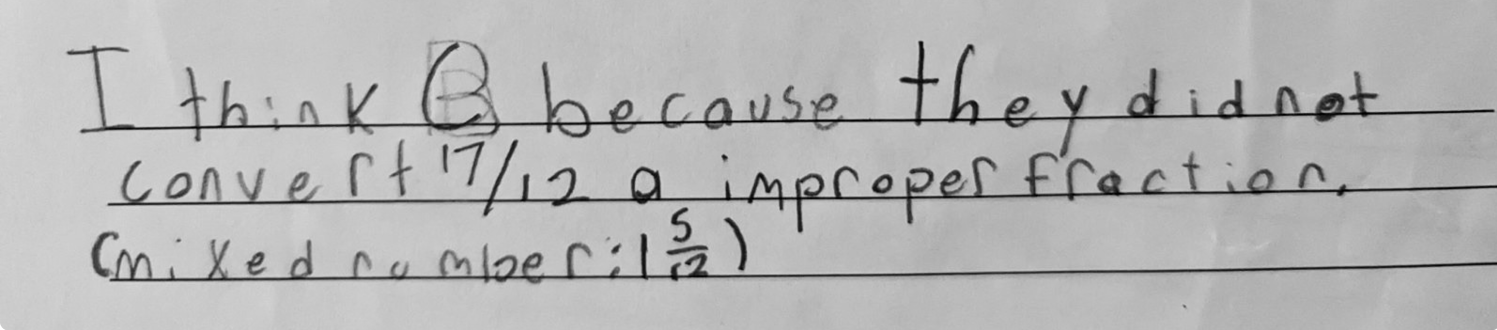


Learning from within the work of teaching
Curriculum materials have shaped my teaching and learning since the beginning of my time in the classroom. They then became the focus of my work at Illustrative Mathematics and now in my current work at Amplify.
I am a strong advocate for high-quality curriculum materials, and at the same time, I also believe that every curriculum can always be improved to better meet the needs of students and teachers.
I continually recognize and appreciate the time I get to spend planning, teaching, and reflecting with teachers about their dynamic and ongoing relationship with curriculum materials.
These opportunities to learn from within the work of teaching are invaluable inputs to our current work at Amplify, where we have the exciting opportunity to improve the characteristics of math resources currently in schools.
Want to learn more from Kristin Gray? Watch her webinar!


